В прошлом посте я рассказывал как поставить Octave, а теперь расскажу о том, что с ним можно делать. А именно о решении систем уравнений.
А если еще точнее, то о системах линейных алгебраических уравнений. Представляющих собой нечто такое:
Спасибо Википедии за красивую формулу.
Такую систему можно представить в виде произвидения матриц:
А если еще точнее, то о системах линейных алгебраических уравнений. Представляющих собой нечто такое:
Такую систему можно представить в виде произвидения матриц:
A*X=B
Матрицы - это основной тип данных, с которым работает Octave. При работе с ним старайтесь по возможности представлять данные в матричной форме.
Разберем решение на примере просто уравнения:
Матрицы коэффициентов и свободных членов для этой системы:
Теперь, когда мы определились с условием, запускаем Octave.
В появившейся командной строке набираем код:
A=[1 3 5;3 1 3;4 1 3]B = [22;14;15]
Следующая волшебная команда даст сразу корни уравнения:
A\B
Главное не перепутать \ и / иначе ничего не получится.
Видите как все просто!
Octave просто сказка. Мне на практике приходилось решать уравнения с 18 неизвестными и это делалось также элементарно.

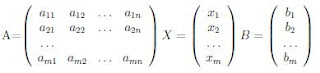


Следующая волшебная команда
ОтветитьУдалитьНикакого волшебства здесь нет, а то, что вы приводите в посте, это не "дубовое" решение системы уравнений - это Least Squares.
То есть A\B это на самом деле (A^T * A)^(-1)*A^T * B
И решается оно, если мне не изменяет память, с помощью быстрого QR Decomposition. Что не просто ни разу.
Главное не перепутать \ и / иначе ничего не получится.
А почему, собственно, не получится?
В данном конкретном примере - в самом деле не выйдет, но такая операция приводит к умножению матрицы A на псевдоинверсную матрицу B. Пример:
octave:8> [1 2; 3 4]/[1 1; 1 1]
ans =
0.75000 0.75000
1.75000 1.75000
и оно же:
octave:10> [1 2; 3 4]*pinv([1 1; 1 1])
ans =
0.75000 0.75000
1.75000 1.75000
Так что автор темнит :-)
Octave просто сказка.
[мрачно] В гробу я видал такие сказки...
Только к третьей версии это убожество научилось запускать матлабовские скрипты хотя бы как-то. Внутри многие алгоритмы реализованы по-разному, оттого выдают на одном и том же коде с матлабом разные значения. Функция plot, и вообще построение графиков - ущебрны, как и те "личности", которые думают, что воткнув гнуплот они всё решат. Задачи теории управления на Октаве не решабельны: нет кучи функций. Да даже такая базовая вещь, как imread, не умеет загружать обычные TIFF-файлы (в 3.0.1 по крайней мере не умел).
Так что про сказку... вы того... рано радуетесь :-)
Уважаемый virens, во-первых, спасибо за первый комментарий, во-вторых, спасибо за подробности, всех этих вещей я и в самом деле не знал.
ОтветитьУдалитьЧто не просто ни разу.
После прочтения и осознания "Ядра Линукс" я решил не задумываться о тонкостях реализации тех или иных решений. Ведь всего одной командой получаем результат. Это ли не просто?
А про устройство надо будет почитать.
[мрачно] В гробу я видал такие сказки...
В своей мирной студенческой жизни я не сталкивался с такими вещами.
Функция plot, и вообще построение графиков - ущебрны
Да, что есть, то есть. У меня gnuplot вообще не работает.
@hooloo комментирует...
ОтветитьУдалитья решил не задумываться о тонкостях реализации тех или иных решений.
И совершенно зря. Октаву и Матлаб писали не боги, и там (особенно в Октаве) полно спорных решений и просто ошибочных реализаций. Нарваться на них очень легко, а потом будете чесать затылок, приговаривая "что за ...?".
Примеры: deconvwnr (вообще алгоритмы деконволюции в матлабе, мягко говоря, спорно реализованы), trusted region LS (оно ведёт себя вовсе не так, как пишет документация), не полностью поддерживаемый стандарт IEEE 754 (ваши floating point calculations округлены будут, но как - никто не знает). И это то, что на памяти.
Ведь всего одной командой получаем результат. Это ли не просто?
А внутри-то как оно работает? А то посчитаете eigenvalues, а оно и не сойдётся с тем, что насчитали руками. И оба ответа, кстати, будут правильными.
В своей мирной студенческой жизни я не сталкивался с такими вещами.
Это пока. Попробуете писать там программы - сказки кончатся :-)
За пост спасибо, кстати. Он меня сподвиг на запиливание своего поста :-)